ギブズ－ヘルムホルツ式

例として 1atmの下でのアンモニア生成について、これらの温度依存性を求めてみる。 しかし、ここでは、これらの量はすべて電池反応の進行にともなう自由エネルギーの 変化分（＜0）とすることにする。

1

ギブズ・ヘルムホルツの式を使った問題。

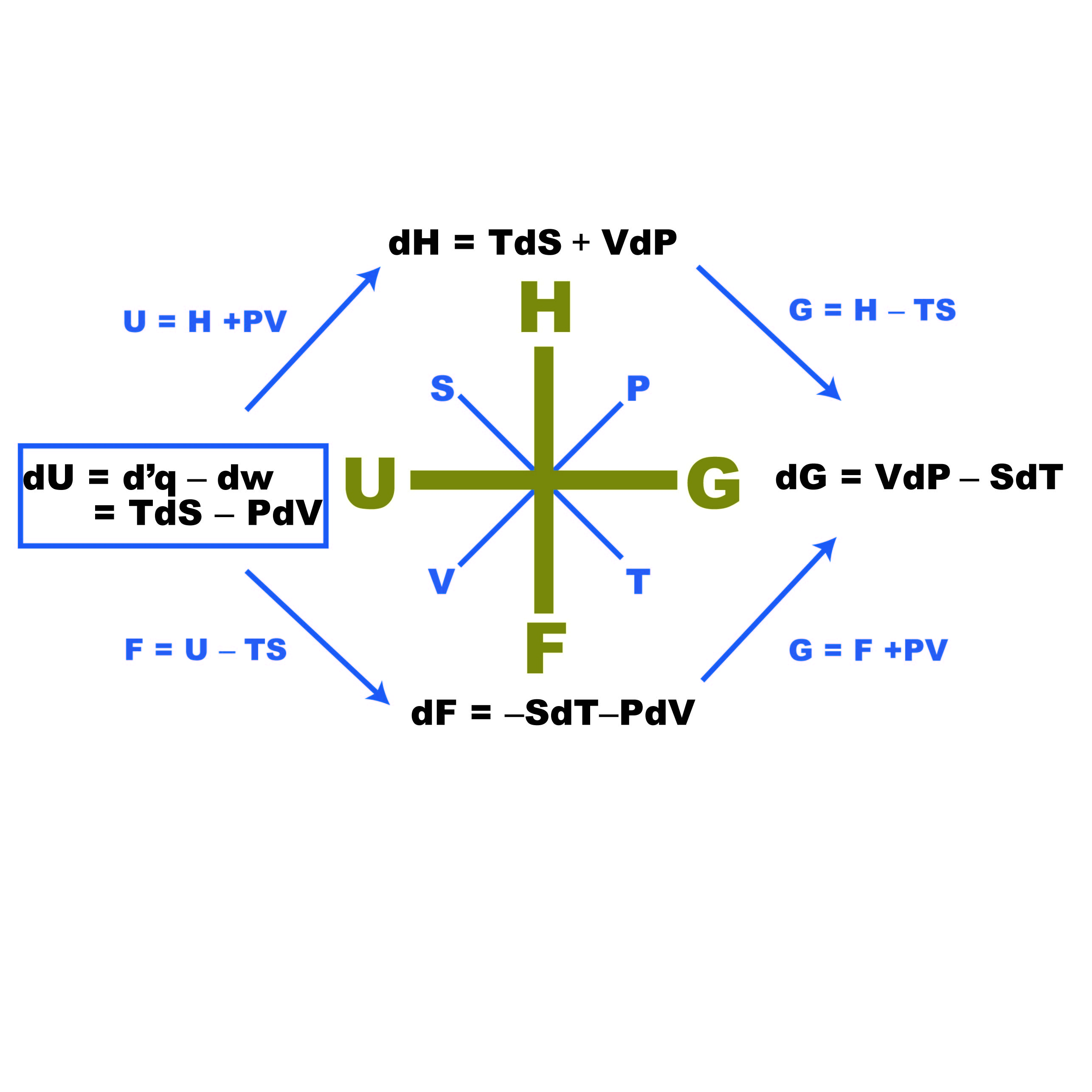
反応物、生成物が標準状態（1atm，298Ｋ）で持つギブズの自由エネルギー値は、別稿で説明したようにして反応熱や比熱のデータから求めることができる。 その具体的な方法は別稿をご覧下さい。 以下、ヘルムホルツエネルギーを例にとって説明する。

電気化学ポテンシャルと熱力学第三法則（ネルンストの熱定理）

そのため平衡定数は以下のように書き換えられる。

20

平衡状態の熱力学（気体の化学反応）

このとき、内部エネルギーの変化分はまさに 定温・定積下に於ける反応熱（相転移熱）です。 一つ目の式は、体積一定のもとエントロピーと内部エネルギーの比が絶対温度になることを意味し、二つ目の式は、一定エントロピーのもと、体積と内部エネルギーの比は、圧力の符号を逆にしたものに等しいということを意味します。 ．熱容量（比熱） 別稿およびで説明したように、定積熱容量と定圧熱容量は と表される。

9

ヘルムホルツエネルギーとギブズエネルギー│大学の化学を探求する 大ケミ

荷電粒子の運動や反応に対する駆動力は電気化学ポテンシャルの勾配できまる。 ［重要な注意］ ただし、ここで としている。 図から解るようにＴ 1よりも遙かに低い温度Ｔ 2に達する。

7

平衡状態の熱力学（気体の化学反応）

また、高温や低温に於ける様子を実験で確かめるのは困難な場合が多い。 エントロピーは状態量ですから初めと終わりが決まれば差は決まります。

3