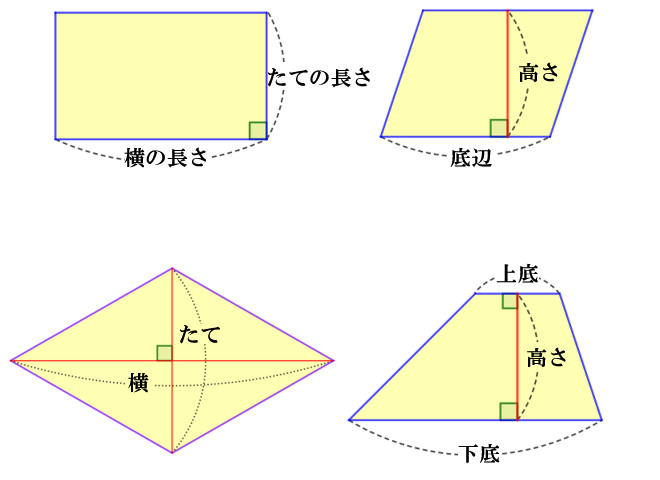
平行四辺形

長方形：対角線が互いの中点で交わる＆長さが等しい• いちいち証明しなくても使っていいよ、ということです。ちょっと変わった六角形さ。

平行四辺形とは？1分でわかる意味、定義、角度、面積、長方形と正方形との関係

$定義平行四辺形$

A B C D E F G 補助線で相似をつくる。平行四辺形の成立条件最後に平行四辺形の成立条件について説明します。

それでは、平行四辺形の対角線は中点で交わることを確認してみよう！「平行四辺形は対角線が中点で交わる」ことの説明まず、平行四辺形に２本の対角線を引きます。

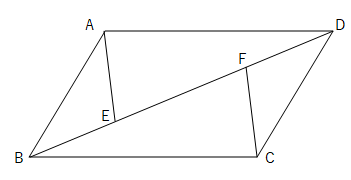
定理（性質）• また、対称の中心回転の軸は、対角線の交点中点に等しいということも特徴の１つです。平行四辺形と長方形、正方形との関係長方形、正方形は、「特別な平行四辺形」です。

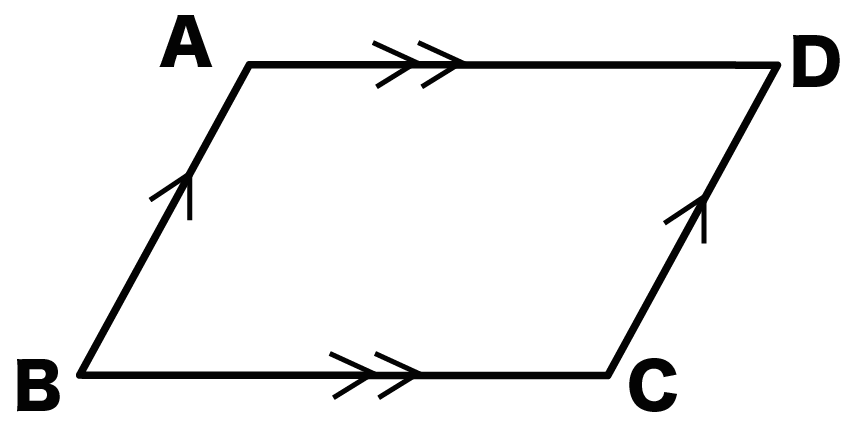
平行四辺形の定義はとても重要なので、次に紹介する性質と混同しないようにしっかり覚えましょう！平行四辺形の性質では次に平行四辺形の3つの性質について１つずつ確認していきましょう。

$定義平行四辺形$

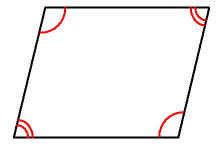
台形台形は平行になっている辺をの長さを足して、それに高さをかけて2で割ったら面積になります。

が他の対角線のを通る（対角線は2本あるが、いずれもこの性質を満たす）。下図のように、平行四辺形に垂直線を引きます。これらは証明をするうえで、「平行四辺形である」といわれた瞬間に使えるヒントになります。

印刷用まとめPDF 最後に今回の内容をPDFにまとめました。 AFの延長線とDCの延長線の交点をHとする。