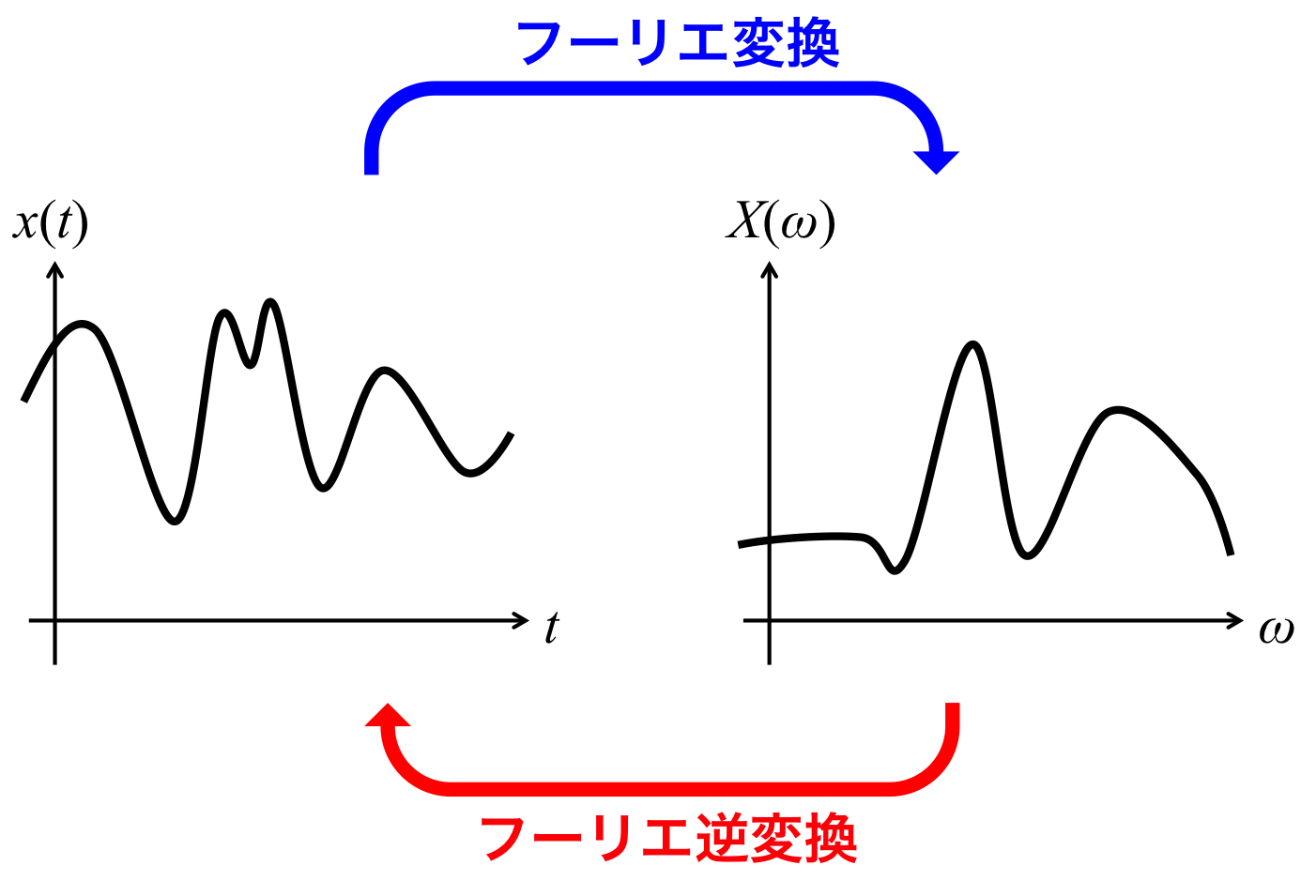
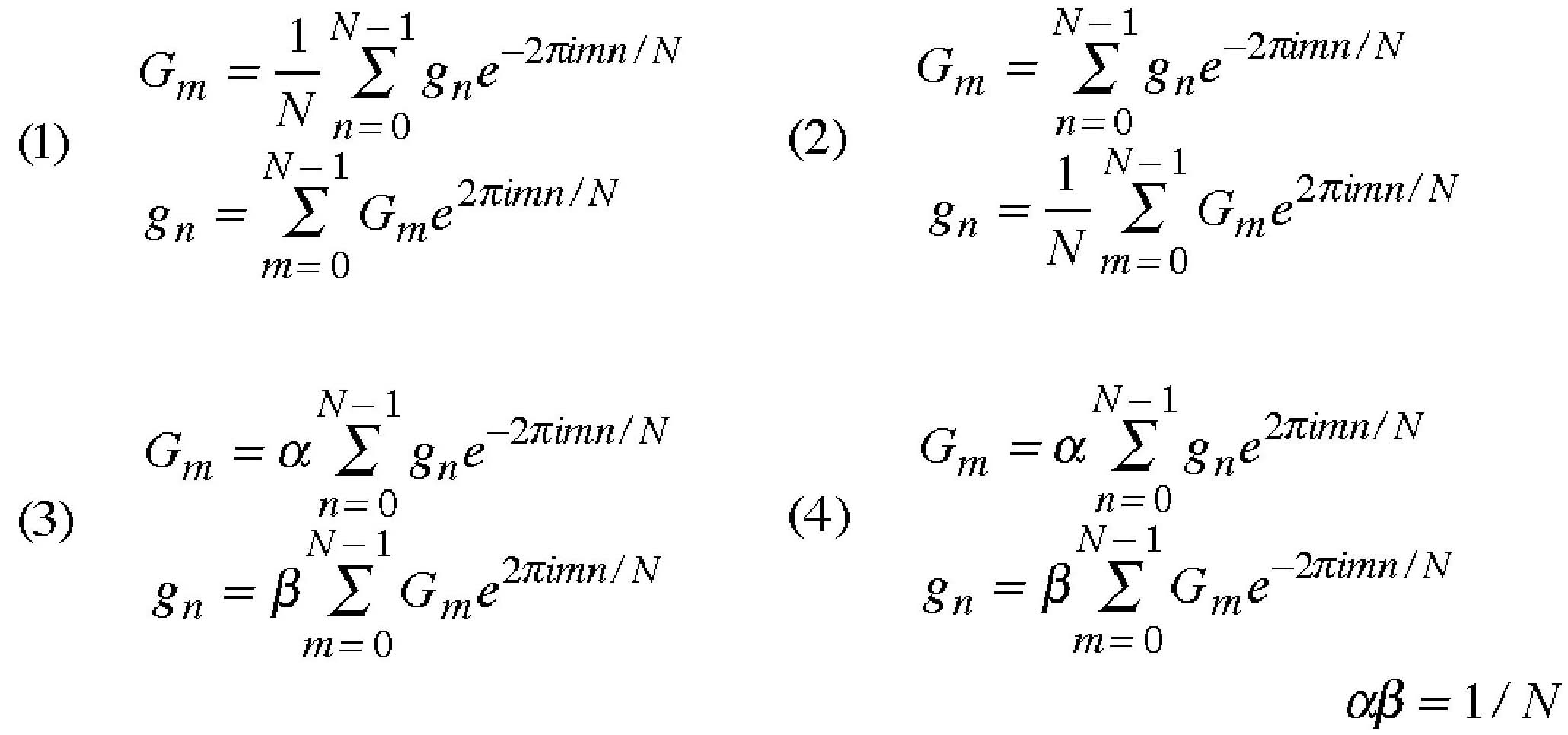フーリエ変換、フーリエ逆変換とは何かを世界一やさしく説明してみた

そのため、パワースペクトルの値は共役になっているのか？いないのか？で実際の波形の振幅と倍、異なるので、注意が必要です。 表示されたウィンドウの入力範囲の部分にある上矢印の部分をクリックします。 フーリエ級数展開とフーリエ変換 Fourier series and Fourier transform フーリエ級数 区間 における，周期 の区分的になめらかな周期関数 のフーリエ級数展開は 1 ただし，フーリエ係数 ， は 2 3 である． 三角関数の直交性 orthogonality に対して，次式が成り立つ． 4 5 6 ただし および である． ～ 式を示す． [] 式右辺に 式を代入すると， 7 を得る．すなわち 式はwell-definedである．同様に， 式右辺に 式を代入することで 式のwell-definednessを確かめることができる． 複素形式のフーリエ級数 に注意すると 8 を得る．ここで 9 などとすると，これらをまとめて 10 とできることが分かる．したがって 式は 11 と書き直すことができる． を複素フーリエ係数， を関数 の複素フーリエ級数という． フーリエ積分 フーリエ級数展開される関数 が非周期関数の場合， とすることによって，フーリエ級数はフーリエ積分と呼ばれるものになる． 式と 式の積分区間を とし， 式に代入すれば 12 を得る． 13 とすると， より， 式の右辺第2項は 14 となる．また，非周期関数 が絶対積分可能である（i. 最もシンプルな例として，ばねの単振動を考えてみましょう。

フーリエ変換

この計算フローには• 上の図の出典は次のリンク先のPDF。 2020年9月26日更新 Mod by:sikino• そもそも i って何？ と以前は思っていたのですが、グラフに表示すると少しはわかりやすいかと思います。 ちなみに、周波数０は波形の山の個数が０個、つまりデータ全体の平均値となります。

フーリエ級数からフーリエ変換を導いてみた

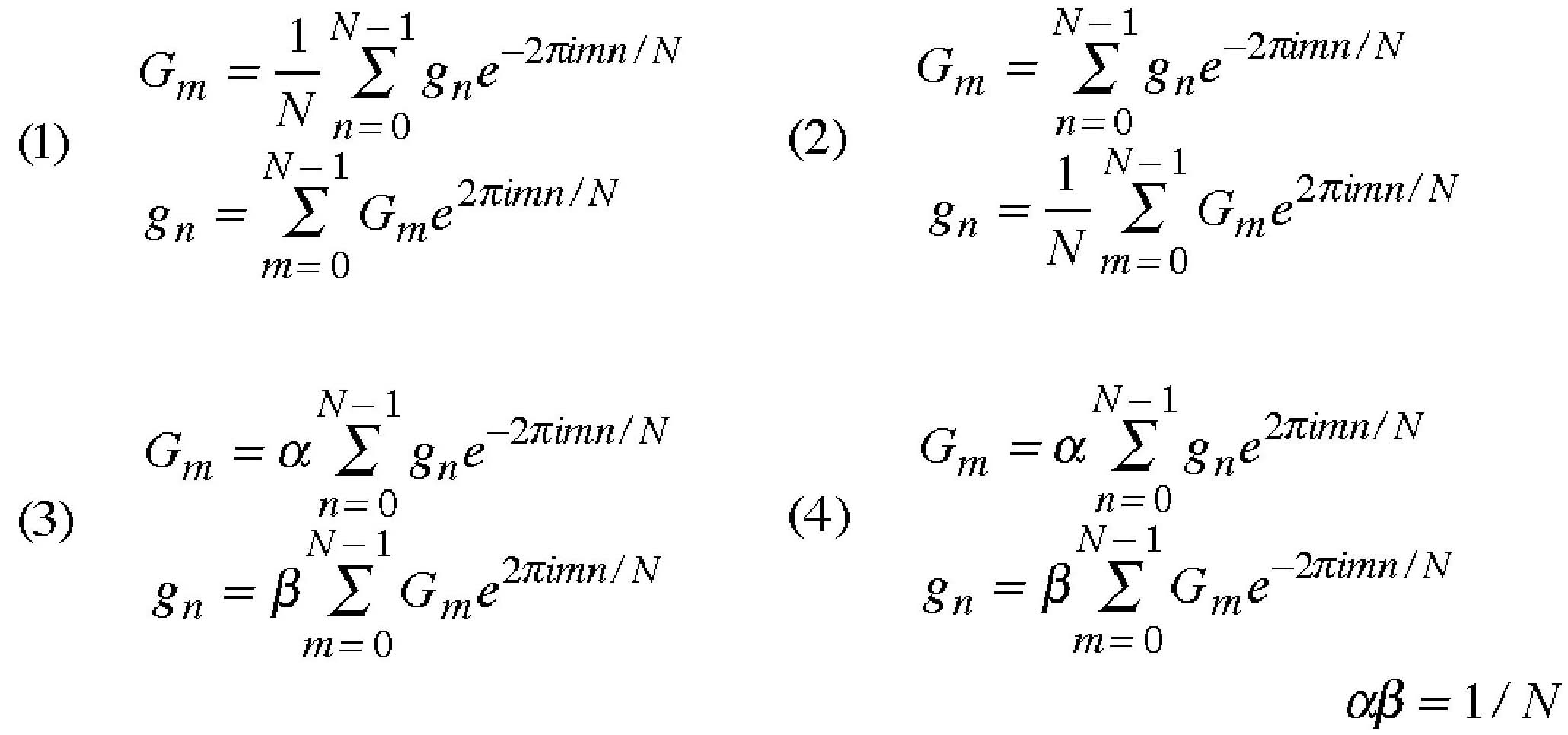
矢印を逆にすれば、元の DFT が分解されていく過程になる• この物理的解釈を最初に理解するのはかなり難しいと思うので（私も最初見たときは全然意味はわかりませんでした）問題にあたって使っていくうちに理解していけばよいと思います。 マイナスの周波数というのは直感的には理解できませんが，数学的に出てきたことなのでとりあえず受け入れて前に進みましょう。

【フーリエ解析03】(連続)フーリエ変換って何？？非周期関数の周波数解析！！【解説動画あり】

ここではExcelの標準の機能であるフーリエ解析について紹介したいと思います。

フーリエ変換の定義と性質

つまり、 に対する係数を得たい場合は、その共役である をかけて積分し、周期で割れば良いことが判ります。

16

フーリエ変換の定義と性質

というのが基本的な考え。

12

フーリエ変換とは？例題1つで簡単に理解する（入門）

2020年11月11日更新 Mod by:sikino• また、 が負の領域まで広がり、正負の周波数で対称的に美しく扱うことができるようになります。 周期関数を扱う• これは1のフーリエ変換がデルタ関数になることを意味しています。 下図を見ると、この様子をイメージしやすい。

20

フーリエ変換の公式 導出：フーリエ級数展開の定義から証明・計算する【フーリエ解析】

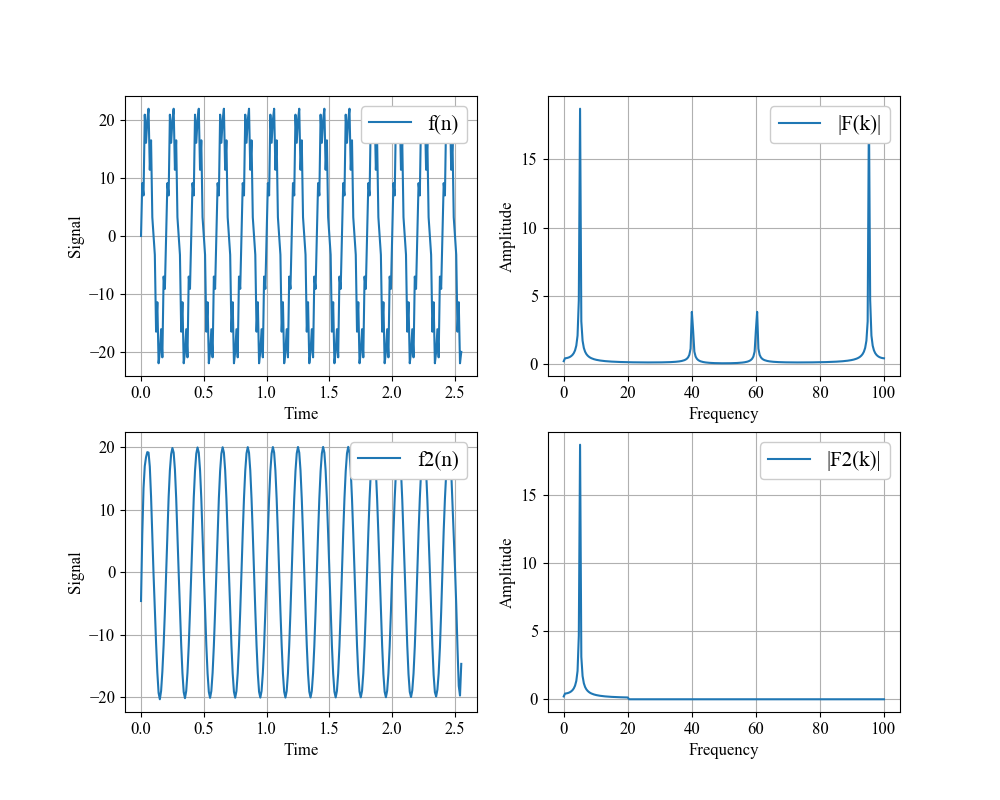
時間によって変化するある関数やデータにおいて，どの周波数からの寄与が大きいかを調べることを スペクトル解析と言ったりもして，幅広い分野で用いられています。 さて，残りの積分ですが，これはガウス積分の公式. 6274169979695i は周波数が２の成分を表してします。 つまり、複素共役になっている周波数（この例では２と３０、４と２８）は２つで１つの周波数を表し、振幅も２つを足し合わせることで、振幅が求まります。

13

1のフーリエ変換

ということを、もう少し詳しく書こうと思ったけど、次のリンク先の記事が秀逸でわかりやすいので、あとはリンクだけ掲載して終わり。 これは単振動の固有振動数に他なりませんね。

7