重回帰分析は安易に使用して良いものではない【Excelは危険】

まずこんな表が出力されます。 05を下回っており係数は意味の有る値であると言えそうです。目的変数は単回帰分析のときと同じで予測値（身長）になります。

回帰分析(単回帰分析)をわかりやすく徹底解説！｜Udemy メディア

しかし、内容は全く異なるものです。

重回帰分析とは｜市場調査ならインテージ

このように分析ツールの回帰分析はあらゆる面決定係数、検定、推定から、分析結果がどの程度信憑性があるものなのか、考える材料を提示してくれます。 Cooks Distance Plot• 解析の目的や、扱う対象となるデータの種類によって、表のように分類できます。

【5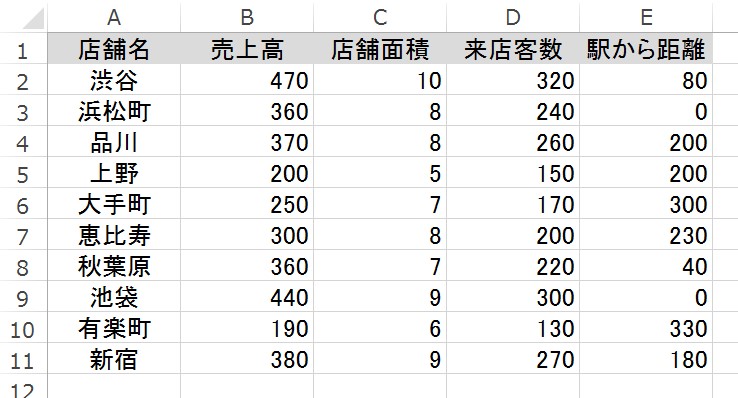分でわかる】相関係数・回帰分析とは【意味・目安・エクセルでの求め方】｜セーシンBLOG

「入力した変数か゛他に入力した変数に影響しているされているかもしれないこと」について。各係数は最小二乗法により算出されます。 x 滞在時間の偏回帰係数・・・8• 「分析ツール」を選んで「OK」を押します。

回帰分析(単回帰分析)をわかりやすく徹底解説！｜Udemy メディア

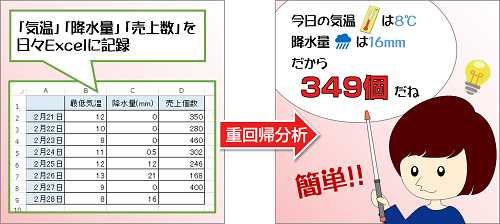
Learnig Curve• 重回帰分析の説明のときに最小二乗法の説明をしますのでここでは省略します。入力Y範囲に「目的変数となる価格のセル」、入力X範囲に「説明変数となる広さ・築年数・最寄駅までのセル」を入力します。そのために１０人分の体重と身長のデータを集めて以下のようないいかんじの直線を書くことをいいます。

重回帰分析とは｜市場調査ならインテージ

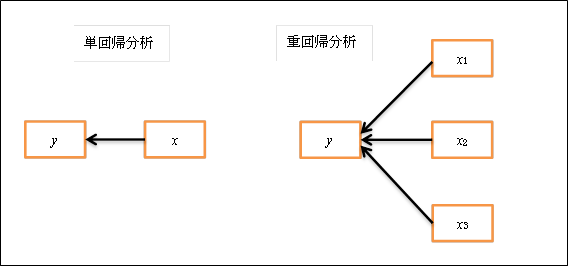
1に近いほど説明変数で説明できる割合が多いことも意味します。機能に優れ、日本語対応。 aとbを求めることができたらxに体重を代入すればy 身長を予測することができます。