06

$最小値次関数最大値二$

どういう考え方をすればわかりやすいですか？たくさんの質問すいません。二次関数の関連記事このように、グラフが動くときも、定義域が動くときも、ほとんど同じ考え方で最大値・最小値を求めることができました。定義域に制限がある場合は、「定義域の端点」「頂点」に着目する。

二次関数の最大値/最小値の求め方(グラフや定義域が動くタイプ)

なので、グラフをカットしたとき最大や最小になるであろう場所が値を含まないになっていると最大、最小が決められない…ってことになっちゃいます。以降省略答え 8 注意点・3で一文字固定以外にもいろいろな解法をあげてみました。このカットされたグラフにおいて最大、最小はこのように見つけることができます。

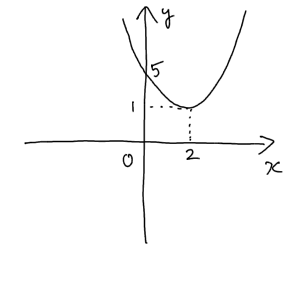
ii のときにおけるこの関数のグラフは、下の図の放物線の緑線部分です。

i のときにおけるこの関数のグラフは、下の図の放物線の緑線部分です。そこで、ここでも a の値によって次のように場合分けしましょう。

そして次にxの値を今求めた値に固定してにして、yを自由に動かしたときに最大値を求めれば、xだけが動いたときの最大値の中の最大値になるから真の最大値を求めたことになるというわけです。ということはtにも範囲があるはず。

グラフを見てわかる通り、下は永遠に続いていますから。定義域に制限がなくても、最大値・最小値の双方が存在するとは限らない。

しかし、これらが思いつくのは全て経験によるものです。（軸から遠い側の）区間の端における二次関数の値が分かればOKです。よっての最大値を求めれば良いわけだ! 定義域に文字を含む場合の解法の手順• 武器を増やして、手入れをしておくというイメージですね。

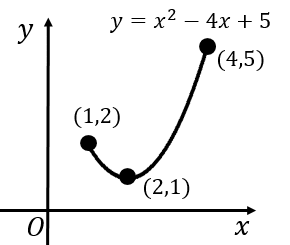
求める方法ですが、慣れないうちはしっかりグラフを書いてみるのがいいです。どういう考え方をすればわかりやすいですか？たくさんの質問すいません。・5で先にyを固定しちゃだめなの? xを動かすというのは、つまり tを動かせば良いということ。