媒介変数表示についてメリットと一覧

が、この問題はそう簡単ではありません。直線上の１点を通り、かつ直線の方向ベクトルとそれとは異なる方向ベクトルで貼られる平面ともいえます。 2019. やりたかったことはこれではないのですが、円との関係がわかったかと思います。

媒介変数表示について｜数学｜苦手解決Q&A｜進研ゼミ高校講座｜ベネッセコーポレーション

ガウスグリーンの定理の証明ガウスグリーンの定理は高校数学では習わないので、答案に使うのは極力避けておくべきです。したがって、閉じた曲線の内側の面積を求める検算のときにはガウスグリーンの定理によってパラメータの端から端まで積分し、もし負の値が求まってしまったらその絶対値を考えればよいことになります。

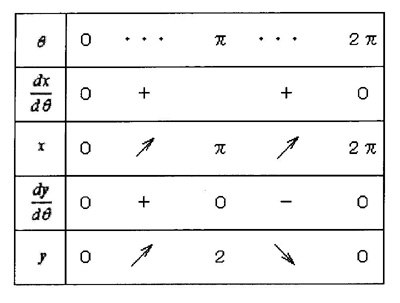
このように、媒介変数表示の計算問題は、表す曲線の範囲が限定されることがあります。

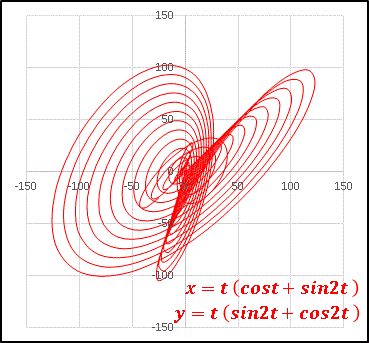
この式の意味をよく考えてみましょう。媒介変数を用いて解かれている常微分方程式の例 [ ] 媒介変数を二つ用いて、求積法により解かれている常微分方程式と、その一般解を以下に示す。

xとyを媒介変数tが橋渡しします。

一方、定点に対して、でないベクトルに平行な直線を考えます。媒介変数表示されたグラフの面積の検算方法媒介変数表示されたグラフによって囲まれた面積の求める過程は計算が複雑であり、計算ミスが頻発しがちです。

$変数表示媒介$

・リサンプリングは2000回以上を推奨＊復元を許したリサンプリング：元のデータから標本を復元抽出（同じデータでも重複して抽出）して、同じサンプルサイズの標本を何度も作ることその他・研究を行う前に、媒介モデルが理論的に想定できることを説明する。