【中２数学】図形の中でも重要なものの１つ、二等辺三角形について徹底解説！

から、残りのＢＦは残りのＣＧに等しい。

3分でわかる！二等辺三角形の定義

対して、「二等辺三角形の２つの角の大きさは等しい」「二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する」のように、定義をもとに証明された事柄の中で大切なものを定理と言います。なお、Ｆ、Ｇを辺ＡＢ、ＡＣ上にとることは、原論第一巻の論証過程においては、証明完了までに至らない。

文字の角度を順にxで表す• （作図. よって、正しくありません。 2つの直線が平行ならば、同位角は等しい。

こちらの性質を利用した問題はこちら。角度によっては、こんなふうに直線じゃなくなっちゃうよね。

三角形の底辺と高さ（中線と中点連結） [ ] 三角形の 3 つ辺のうち一つを選んで底辺とし、その対頂点から底辺（またはその延長）に下した垂線から、三角形が切り取る線分（線分の長さ）を、三角形の高さという。

こちらは、後に出てくる練習問題1で例題を確認してください。 2辺の長さが等しい三角形• 角度によって定義された三角形・直角三角形…１つの角が直角である三角形・鋭角三角形…３つの角がすべて鋭角である三角形・鈍角三角形…１つの角が鈍角である三角形三角定規に代表される直角三角形。任意の点をとる）による。

二等辺三角形の性質をもとに、順番に求めていきましょう。もし判断に迷ったら、ぜひ、個別指導のプロにご相談ください。頂角の二等分線は、底辺を垂直に二等分する。

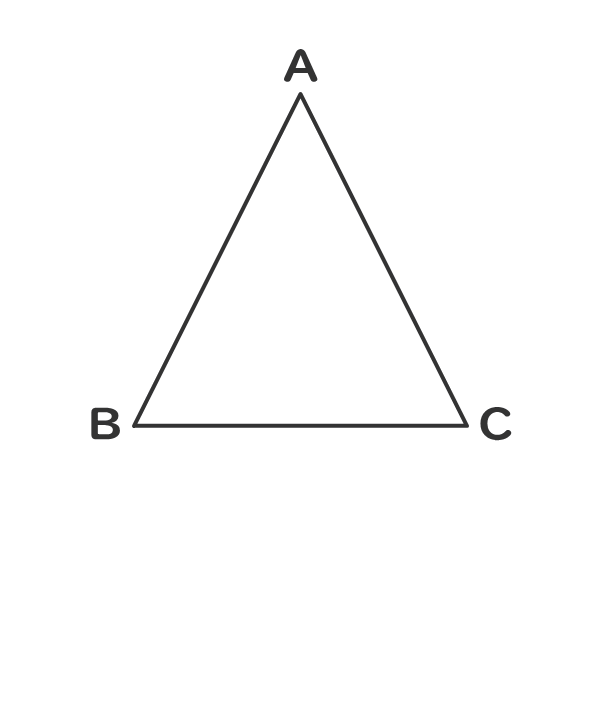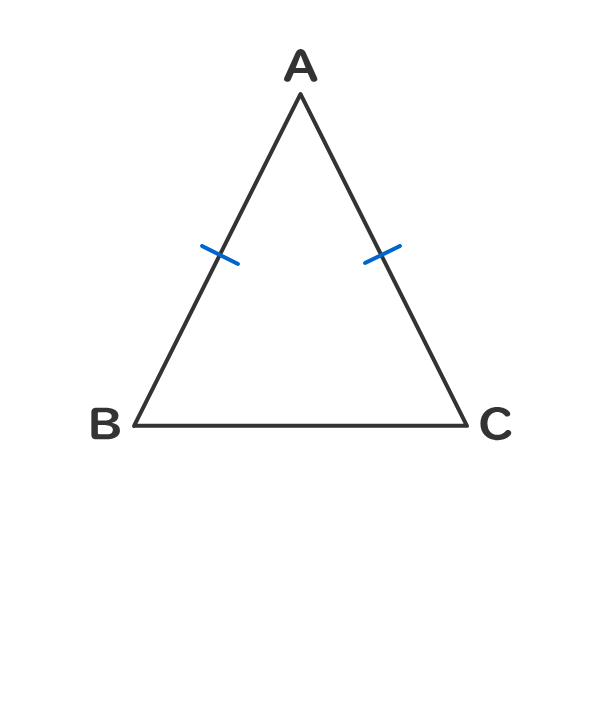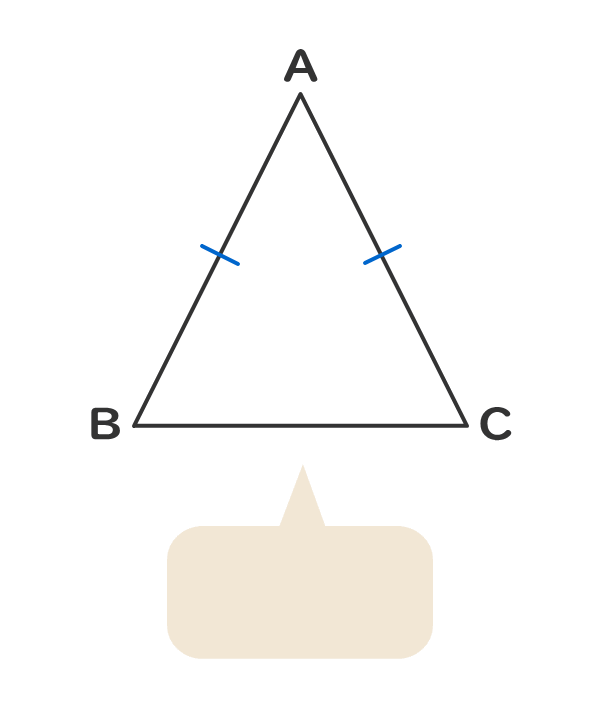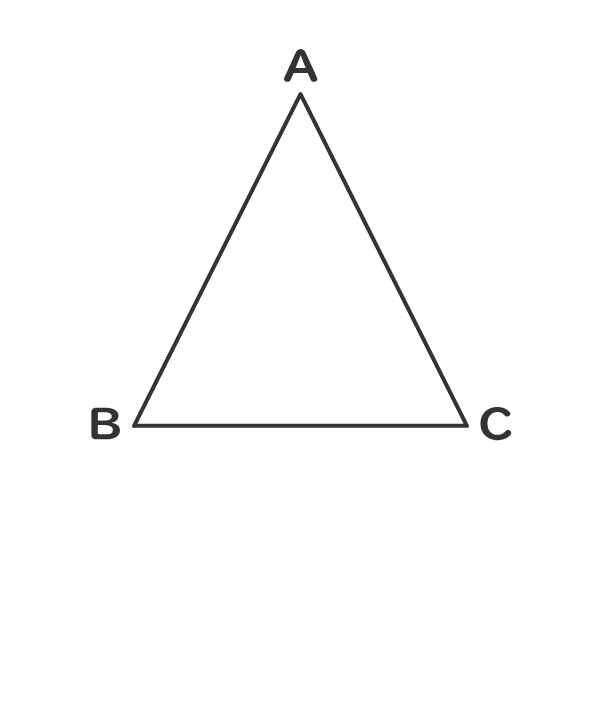
例えば二等辺三角形なら、2辺が等しい三角形のこと。による。二等辺三角形は2つの定理（性質）がありますが、これらは三角形の二辺の長さが等しいことに由来します。