ボレル集合

$集合ボレル$

」「 I n 」：このような区間の全体を I n と記す。こんな操作。即ち、各性質、定理に関して、以下のような違いが存在する。

ボレル集合族って何ですか？？？

$集合ボレル$

（数式は、定数倍したり、足し算したりできますよね）数式に対して「絶対値」とか「長さ」と言ってもピンと来ないですよね。

ときわ台学・ルベーグ積分

f z の特異点における留数を求めたい場合は、f z と求めたい特異点の極を求める必要があります。 A ベストアンサー MANIFESTさんがどのくらいの予備知識をお持ちなのかわからないので答えにくいのですが、集積点について質問されると言うことは少なくとも位相空間についての基本的な用語くらいはご存知だと仮定して説明します。

測度論 / ルベーグ積分

たしかに、Rは、覆っていませんでした。あまり、触れないように避けたのですが、Rって、実数集合のことだったんですね。測度０の集合（＝零集合）を、の計算結果には影響しない余計な部分として削ぎ落とすために、予めの土台となる測度空間に備わっている性質という意味で、完備測度の要件になってる。

ボレル集合体とはなんぞや

すみません。カントール関数は連続なので2の像はボレル可測ではないこれがボレル可測なら1もボレル可測になってしまうあと、検索したら非ボレル集合の構成方法がありました。（０でも無限大でも、定まっていれば長さです）ここまではえがける図で表現できます。

シグマとボレル集合族と確率測度

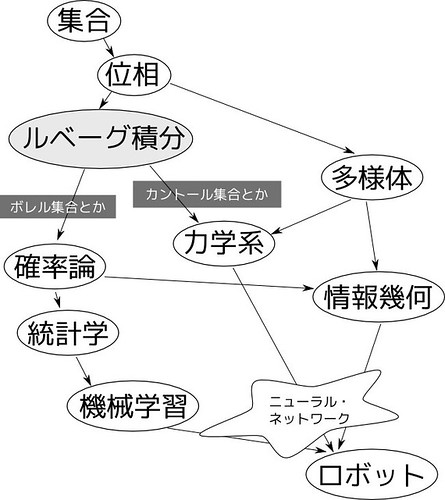
別に、i. これらが全てPの定義域として閉じてますよ、という要請を追加した開集合のような物がシグマ集合族だ。こうすることで、をより、一般的で広範囲な対象のものとして扱える。

Rのボレル集合族はR上の区間(a,b]全体からなる集合を含む...

例えば数直線（一次元）を全体集合とする場合で考えましょう。 d x,y は０以上であり、０のとき、xとyは等しい。なんだそりゃ。

ボレル集合体とはなんぞや

そこで、次の事実を使う。上図から分かるように、不連続点が寄与する分割長方形の面積は、リーマン時の幅を無限に細く取る操作で、無限に小さく出来るので、無視できる。そこで、関数列の収束を扱う前段階として、以下のような各点収束、概収束の概念を導入する。