二倍角、三倍角公式、半角公式

バンザイ！. 太陽が沈み、寒くなった情景を思い浮かべながら唱えると覚えられると思います。

オイラーの公式とド・モアブルの公式と三角関数の n 倍角の公式と

それだけです。これを三角関数を用いて書くと以下のようになる。下のボタンから、無料体験のお申込みが可能です。

例えば haversine は球面上の2点の距離を求めるのに使用された。

指数法則が使えるのもミソですね。（2）加法定理と三角関数の相互関係を用いて整理する。三角関数から求められる versine, coversine, haversine, exsecant などの各関数は、かつてなどに用いられた。

$の公式倍角三$

もう少しの公式シリーズ（）。この記事でもベタに加法定理や倍角の公式を導いてみます。

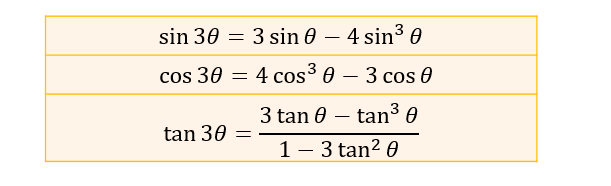
（応用）三倍角の公式の導き方三倍角の公式も加法定理と二倍角の公式使うことで導き出せます。 3倍角の公式の使い方公式を覚えて、証明の仕方も学んだところで実際に3倍角の公式を用いた問題を解いてみましょう。半角の公式の導き方今度は半角の公式です。

三倍角の公式の右辺を因数分解して合成を行うことでも証明できます。では実際にやってみます。 setAttribute "aria-label","Close" ,P. 倍角の公式次は倍角の公式。

二項係数（組合せ数）をとして、以下の公式が成り立ちます：二項定理をもう少しド・モアブルの公式を使っての倍角の公式を導くには、を展開して実部と虚部にまとめる必要があるので、を展開して（単位を含む）の偶数冪と奇数冪にわけてまとめる式を導いておきましょう。