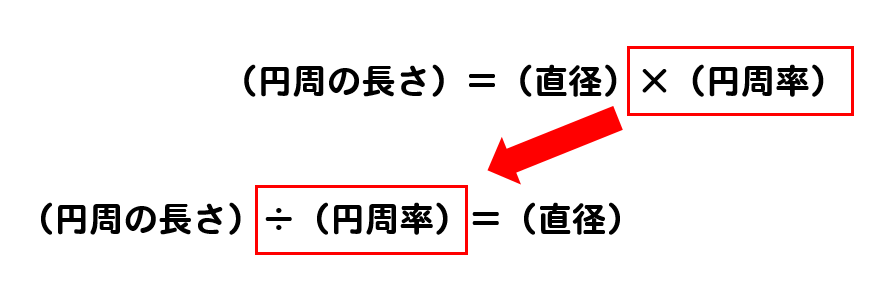
円周の求め方

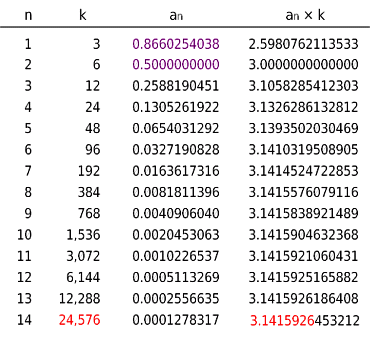
累乗の項の和）が、nを大きくするととなることこれについてはをご覧くださいを使って、という結論を得ていますが、これだけでは規則性がわかりません。 1415 9264 8777 6988 6924 8 と小数点以下21桁まで算出している。

東大入試も解ける！？中学生の知識で円周率を求めてみよう！

物が回転するときの回転速度を周速（度）と呼びます。

）が必要です。また、菊池は翌年にも『東京数学物理学会記事』第8巻 1897 に建部賢弘による弧の長さの計算法を紹介する論文を書きました。

スーパーコンピュータや性能の高いコンピュータを使って円周率を計算させています。確率実験から円周率を導き出す 1600年代には変わった方法で円周率を求める方法が考え出されました。その後にもう少し正確な円周率の計測方法が生まれます。

円周率は既約分数で表せない、無限に続く循環しない小数、つまり無理数であることが証明されている。

ルドルフは、小数点以下35桁までを計算した。これはこの方法を使う限界の精度です。 4 なぜ、ループせずに無限に続くのか。

正多角形や円の世界ではこういった数がよく出てくるなんて不思議だな～」くらいには理解していただけたのではないでしょうか。このの概念はに出版されたド・モアブルの『巡り合わせの理論』に現れている。

153846153… になったよ！おめでとう。

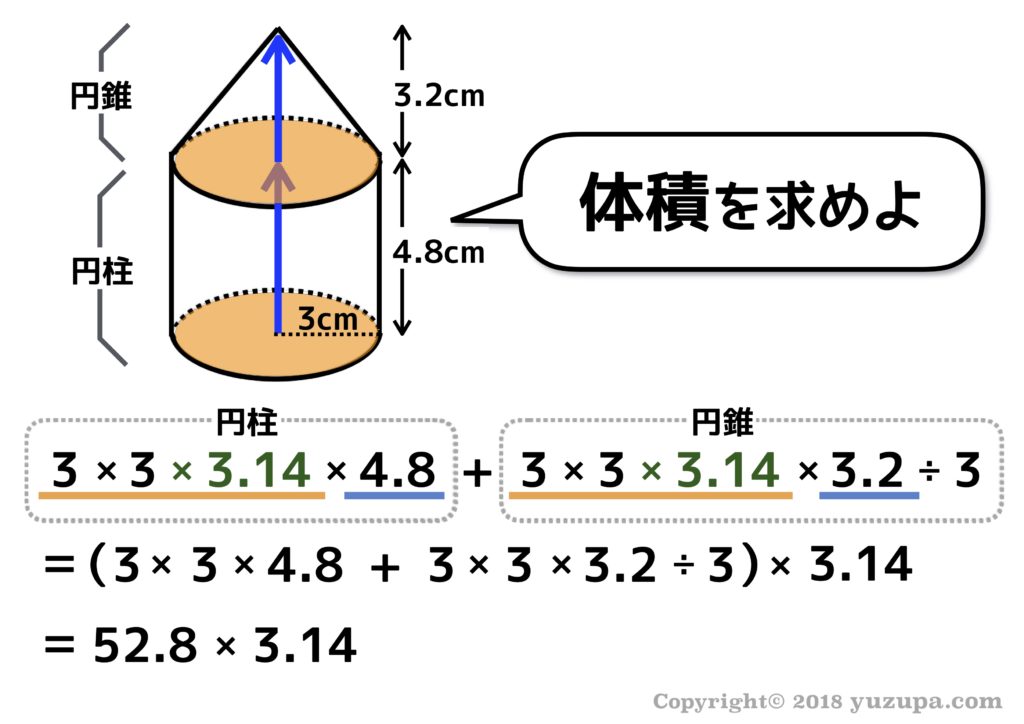
その最初のテーマの一つが円周率を数学的に計算する努力であり、1663年に日本で初めてが『算爼（さんそ）』において「円の内接多角形の周の長さを計算する方法」で3. 16という値を引き継ぐようになってしまった。円周率を求めるなんて、すごいね… 紀元前2000年頃。