3. フーリエ変換 (やる夫で学ぶディジタル信号処理)
他にも多様な応用方法がありますが,それぞれの状況ごとに説明ページを書いていきたいと思いますので,そちらを参照していただければと思います。
7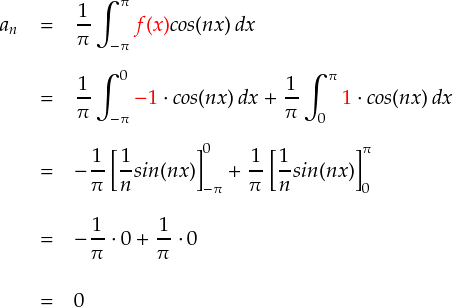
物理で出てくる微分方程式への応用 さてフーリエ変換そのものに興味がある人は専門書等をあたってもらえれば無限に詳しく書かれていますが,これからは物理学におけるツールとしてのフーリエ変換を見ていきましょう。 2020年10月18日更新 Mod by:sikino• フーリエ変換の物理的意味 変換の式を見て「これは一体何の意味があって何の役に立つんだ」と思った人も多いかと思います。
17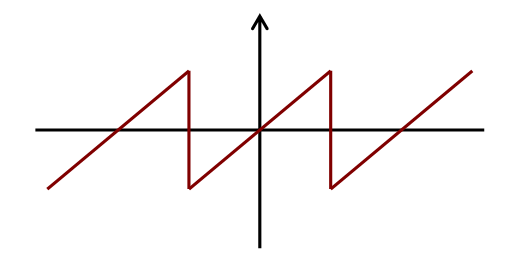
Windows10 64bit• このような時,関数を分解したときのそれぞれの周波数の寄与度は係数で表現できそうですよね。
1
私が現在勉強しながら研究している非線形性に関する理論を簡単にまとめておきます. もちろん,まだ一回も発表もしていない研究の内容をそのまま書くのはさすがにいけないので,ここではすでに世間ではよく知られているような内容のみをまとめておきます. 表記について• fft でできます. グラフ描画は離散データなのでstemで描画するためnp. 2020年9月26日更新 Mod by:sikino• この変換をグラフで表すと以下のようにになります。 このことが、この関数がバンドパスフィルタと呼ばれる所以で,この関数を使うことにより解析したいデータのうち小さな周波数成分だけを取りだすといったことが可能になります。
2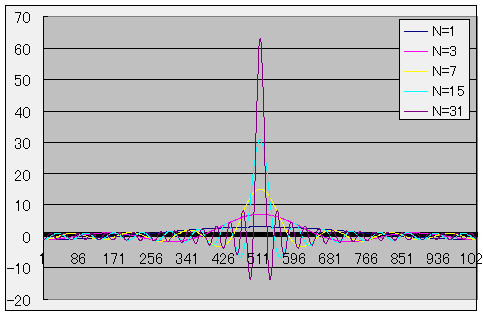
競技プログラミングにおける畳み込み演算のアレコレ(e. 符号違いの同値が交互に出てくるので次のようにまとめることが出来ます. 時間によって変化するある関数やデータにおいて,どの周波数からの寄与が大きいかを調べることを スペクトル解析と言ったりもして,幅広い分野で用いられています。 2020年9月26日更新 Mod by:sikino. , , をそれぞれ, の振幅スペクトル,位相スペクトル,パワースペクトルと呼ぶ. やる夫 あれ? やる夫 えっと,周期的な時間信号をいろんな周波数成分に分解するんだったお. やらない夫 そう,その「周期的」ってのが重要だ.じゃあ周期的じゃない信号はどうするの? そういえば数学の教科書では角周波数は小文字で って書いてたと思うお.どうして大文字で書くんだお? 特別な関数のフーリエ変換 一般の関数のフーリエ変換はそう簡単に求まりませんが,ここでは頭に入れておきたいいくつかの有名なフーリエ変換を紹介します。
10
事前に必要となる知識の説明(,)• は角周波数を表す連続変数である. は に含まれる角周波数 の振動成分の量 振幅・位相 を表す.• ここからフーリエ級数を導出する。 3 フーリエ変換などとの違い 文脈などによっては フーリエ変換 と言って 高速フーリエ変換 FFT や 離散フーリエ変換 DFT の事を指すことがありますが,純粋な フーリエ変換 は FFT とも DFT とも違う計算を指します(原理は似てはいますが). フーリエ変換と名前に付く,似た変換は以下の4種類があります. 時間領域 名前 周波数領域 連続 周期的 フーリエ級数展開 離散的 非周期的 連続 非周期的 フーリエ変換 連続 非周期的 離散的 非周期的 離散時間フーリエ変換 連続 周期的 離散的 周期的 離散フーリエ変換 離散的 周期的 周波数領域とか,周期的・非周期的 とか良く分かりませんね. 今は分からなくてもいいですが,このような特性の違う変換があるということを覚えておけば良いです. フーリエ級数展開から説明をするのが一般な気がしますが,今回は直接離散フーリエ変換の解説をします.(個人的にはフーリエ級数展開よりも離散フーリエ変換の方が理解しやすいと思います) 2. の順番で説明します. 1. もちろんこれは複素関数を積分しているので,一般には変換後は複素数になることに注意してください。
8まとめ フーリエ変換を行うことで、 異なる波数の波がどれくらい含まれているかが知ることができる。 手前に余計な係数がくっついてきますが,覚えてあげましょう。
5