円すいの展開図、側面積の求め方！公式を使って15秒で解こう♪

扇形の中心角は、完全な円に対してどれくらいの割合の大きさなのかを示した値です。

【中学数学】円錐の側面積の求め方と公式【図でわかる！】

次の円錐の体積と表面積を計算しましょう。

（2）この円錐の表面積を求めなさい。ここまできたら側面だけを取り上げて考えてみます。ただいずれにしても、このように計算しなくても、小学校の算数や中学数学であっても直感的に立体の体積を理解できます。

では、下の図のように、半径がr、母線がmの円錐を例に、底面積と側面積を別々に求めていきましょう。または中心角を出した後、扇形の面積を計算することもできます。

一方で円錐の側面積はどう計算すればいいのでしょうか。母線から考える、円錐の中心角の求め方一方で中心角が分からない場合はどのように計算すればいいのでしょうか。こうして、以下の公式が成り立つと証明できました。

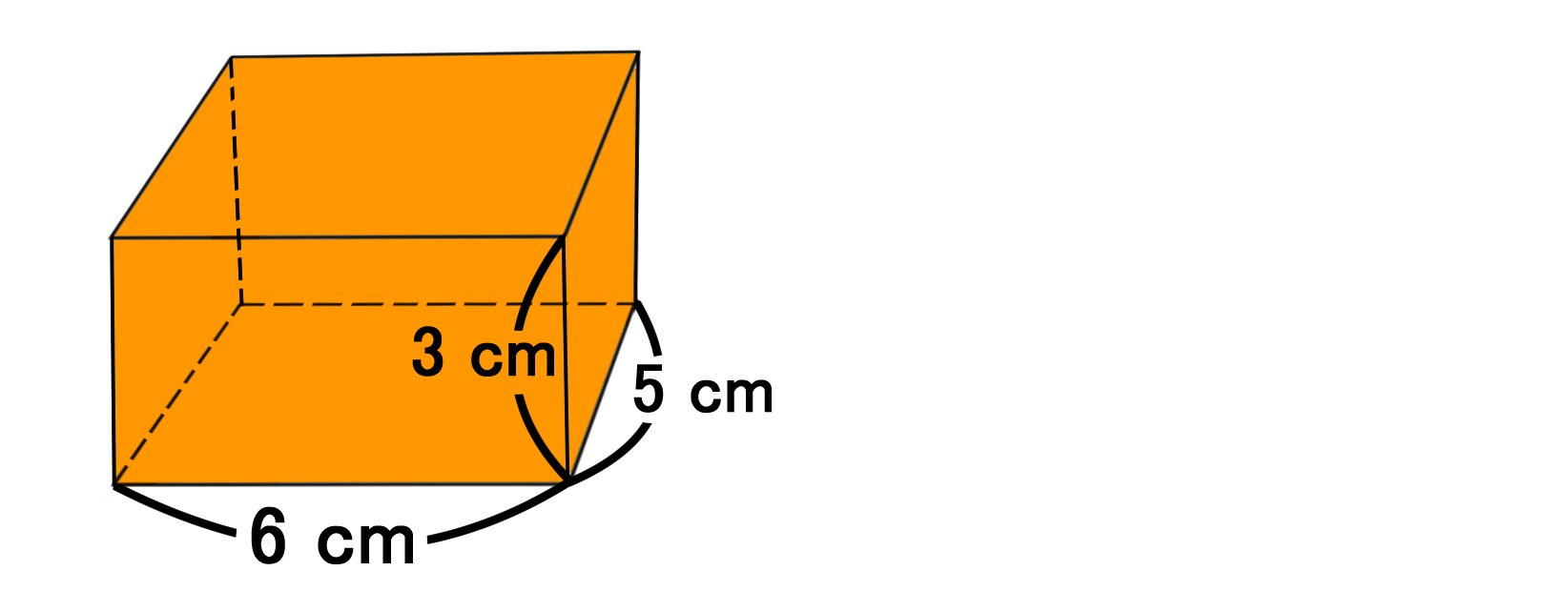
展開図を書くと底面は円で側面は扇形になります。上の図で表したように、側面のおうぎ形の弧の長さと、底面の円の円周の長さを等しくしなければ正しく立体が作れないためです。

展開図はくっつけられるはずなので、赤と緑の長さは等しいです。