3次方程式まとめ(解き方・因数分解・解と係数の関係)

因数分解の基本的な公式 因数分解でまず大切なのは公式です! 考えながら因数分解をしていると時間がかかりますが、 公式に当てはまる形であれば考える間もなく答えを出すことができます! 最大の共通因数(すべての項に共通の因数)でくくる• 項が三つの場合、真ん中の係数を半分にした数が右側の項の平方根かどうか? という順番で解答を進めると比較的スムーズではないかと思います。 x 2 の項の係数の正の約数との約数を組み合わせて x の項の係数を作る。
【新規開拓】成果最大化のための因数分解|zin|note

こういう場合は(3a+? 3a+?)まずはこの形を考えてみるといいですね。
5
因数分解とは
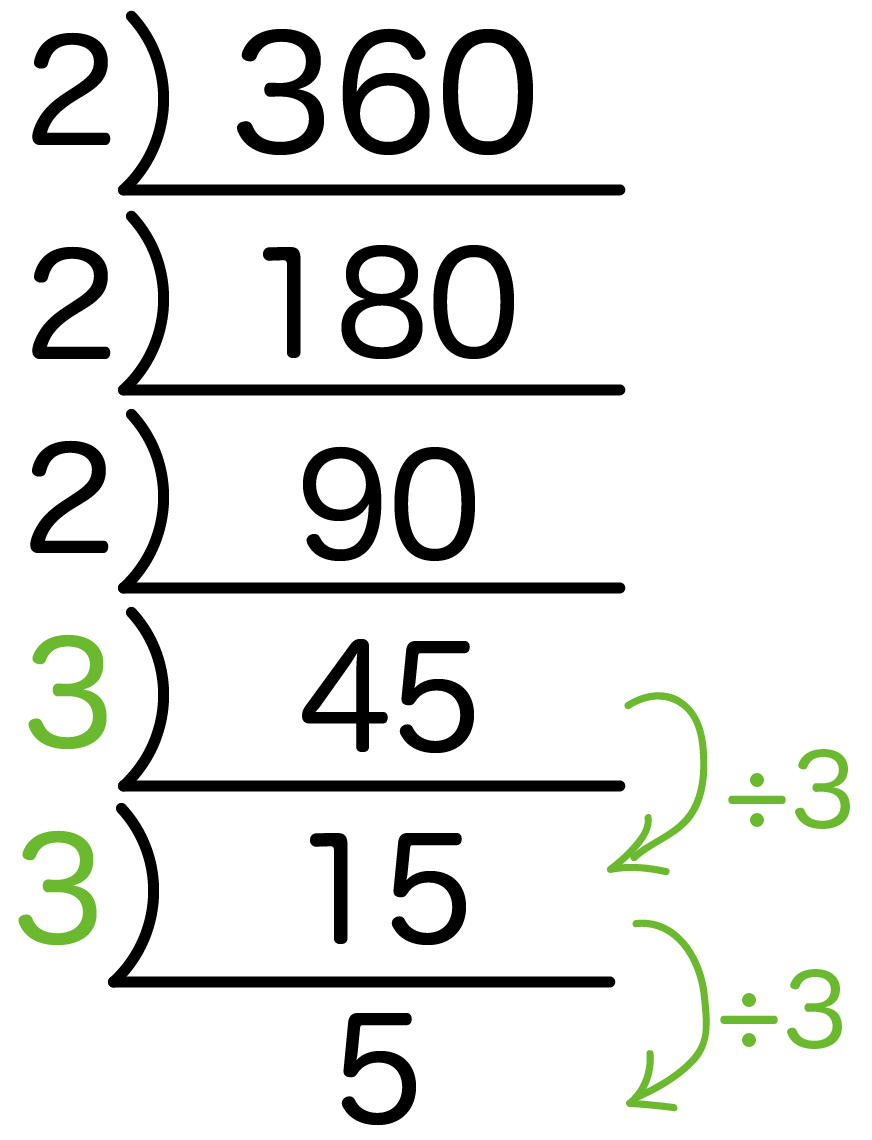
【例題】 【STEP1】 まずは係数を書き込みましょう。 公式を使えれば因数分解は楽勝です。 すると下の図のようになるのがわかりますか? これが書けたら次の図のように上の式と下の式ができますよね。
12
【公式いろいろ】因数分解のいろいろな問題とその解き方|スタディクラブ情報局

与えられた式を、公式が適用できる形に変えるために共通因数でくくるという作業をする必要があります。 因数分解とは さて、因数分解がどういうものかはなんとなく分かってくれたかと思います。 なお、対象が自然数の場合、「約数」、「因数」、「因子」は全て同じ意味になります。
5
因数分解機

精神的に強くなる などなど、勝つために必要なことをいくつも思いつく人の方が往々にして強いですね。 因数分解の応用問題 基礎的な因数分解の公式は以上です。 ただし、やはり公式は覚えてしまったがテストでは有利です。
16
因数分解 ~中学3年生の数学~

「展開」の反対ですね。 変数はすべて x(半角、大文字小文字どちらでも可)です。 有理数係数の多項式環における既約因子分解には、効果的な計算機アルゴリズムが存在している。
因数分解
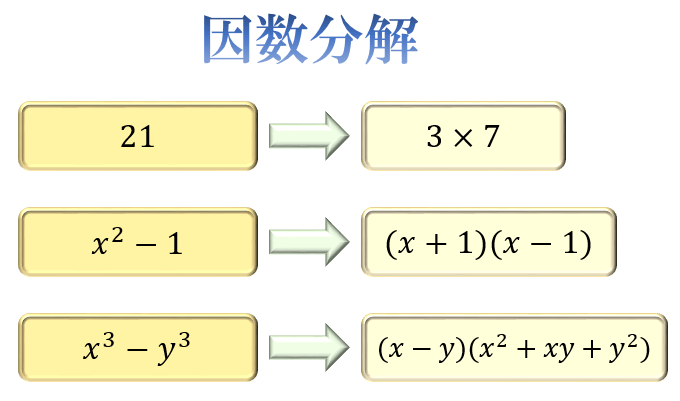
多項式の因数分解をする場合、 「カッコ中は1以外の共通因数がない状態にする」という暗黙のルールがあるため、最大の因数で括る必要があるのです。
9
因数分解の意味・問題の解き方|数学FUN

このあたりは習慣なので、習慣に従うようにしましょう。
1
中学数学 因数分解!基本から発展問題まで
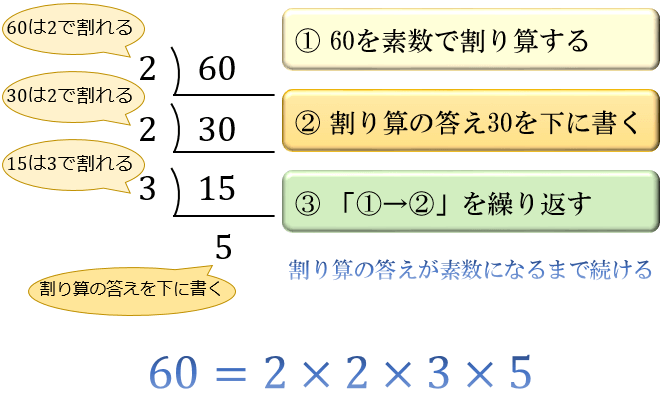
これは最も簡単な因数分解の 1 つです。 公式は実際に問題演習を通じて覚えるとスムーズです。 因数分解は展開とは違って、やり方を分かっていなければできない問題なのです。
14