回転行列の性質と実ベクトルを回転させる証明(2次元・3次元)
まず、z軸を回転軸にした3次元回転を考えてみましょう。 回転軸の方向ベクトルは、次項に示すように固有値問題を解くことによって求めることもできます。
12
まず、z軸を回転軸にした3次元回転を考えてみましょう。 回転軸の方向ベクトルは、次項に示すように固有値問題を解くことによって求めることもできます。
12
このとき、パラメータに無駄な自由度があるとそれを抑えるための制約条件を加える必要が出てきますが、制約付きは制約なしに比べて複雑になるので計算コストが高くなってしまいます。 気になる方は、 を代入したとき(右手系)と、 を代入したとき(Y軸反転の左手系)を比較して、 のY成分の符号だけが反転することを確かめてみてください。 h(サンプルなので打ちミスはない) include "DxLib. (上記で言った、向きと大きさ(始点と終点の関係)のことです。
5
時は、角を滑らかに変化させても、ある姿勢から別の姿勢へと滑らかに変化させられない場合があります。 そこで、式 6 の代わりに、次式を用いることもできます[1]。 対象読者: 3次元 ベクトルの,2次元の回転行列を理解している人. 大学1年の物理数学レベル テンソル解析の初歩 具体的にはを用いた3次元外積の表現 を知っていればなお良い.• この記事では、これら4つの表現方法について• 3次元の内積 ここで、任意の2ベクトルを、内積を保ったまま、 平面内に回転変換できることを示します。

左辺は極座標基底での成分表示になっています。 で利用しやすい 上2つの特徴は、姿勢に関するを解くときに非常に重要になります。

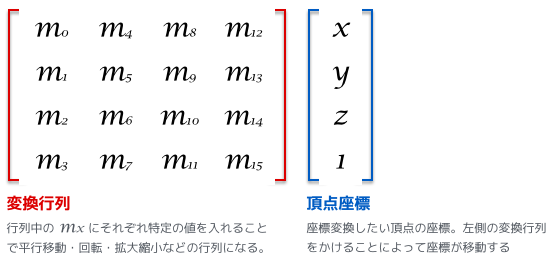
行列変換しない軸に関しては単位行列でそのまま残します。 ) 回転行列 三次元の回転行列の前に のおさらいです。 ちょっと待ってください。

工学の分野では、三次元空間にあるオブジェクトの姿勢を考えるとき、どこか(例えば地面)に基準となる 世界座標系を、オブジェクトに固有の ローカル座標系を設定してその関係を 回転成分・ 並進成分で記述するという考え方をします。 オイラーの定理および回転軸と回転角 剛体回転に関するオイラーの定理は、「一点が固定された剛体において、固定点周りのどのような回転変位も、その固定点を通るある軸周りの一回の回転によって到達できる」ことを保証しています[1]。 初めに述べたように、3次元ベクトルの回転にはいくつか方法があり、それぞれに長所短所があります。
14