有理数とは?無理数とは?定義を明らかにして√が無理数と証明する【数学IA】

41421356 と。
10
参考文献 [編集 ]• こっちも試しにルート2の小数のケタをかきなぐってみると、 1. そうは言っても、無理数にピンとこないね?? 無理数の具体例をみていこう! 無理数の例1. 「自然数に変換できない平方根」が無理数であることを説明するには高校の知識が必要になりますが、一応は中学生でも理解できるはずです。

無理数の例2. 中学数学で扱う2つの無理数• ここで覚える必要はありませんが、数には他に以下のようなものがあります。 (「ゲルフォント=シュナイダー」の定理は、超越数を判定するための奥義みたいな定理です。
17
わかってしまえば全然怖くないので簡単なものから数学の問題を解いてみてくださいね。 それ以外はすべて有理数となります。
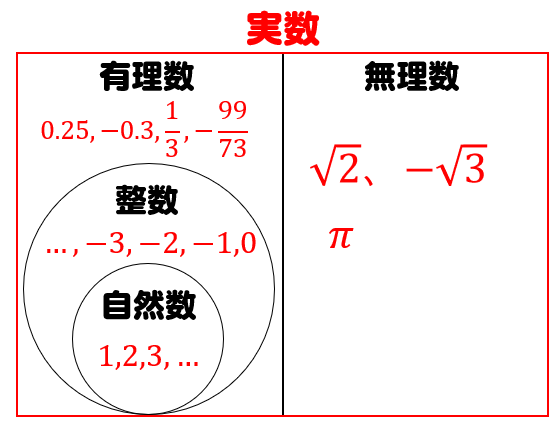
直径と円周の比ののことだったよね?? じつは、これ、 無限に続いてる小数で(無限小数)、 しかも、 その続き方に規則性がまったくないんだ。 「 小数点以下の値が循環している小数」です。 だから証明したいことは間違いではなく正しい」という証明方法です。
7
至る所に有理数もあるはずなのに,無理数では連続になるということですがイメージがつきません. 吉田武『の贈物 人類の至宝を学ぶ』、2010年• 有理数、整数の詳細は、下記が参考になります。 「Aのことを〇〇と呼ぶことにしました」という宣言なので、理解することというよりも、覚えることです。 しかし、なぜ非循環小数は無理数なのでしょうか。
9